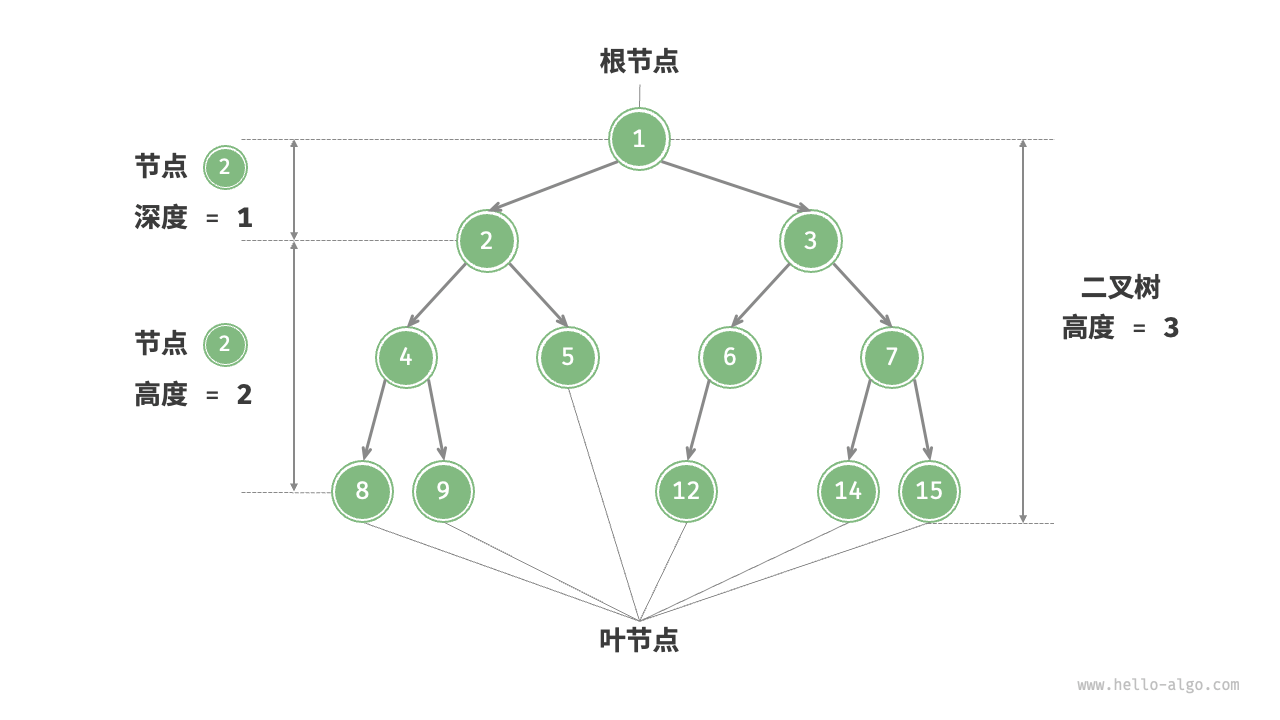
二叉树常用术语
- 根节点(root node):位于二叉树顶层的节点,没有父节点。
- 叶节点(leaf node):没有子节点的节点,其两个指针均指向 None 。
- 边(edge):连接两个节点的线段,即节点引用(指针)。
- 节点所在的层(level):从顶至底递增,根节点所在层为 1 。
- 节点的度(degree):节点的子节点的数量。在二叉树中,度的取值范围是 0、1、2 。
- 二叉树的高度(height):从根节点到最远叶节点所经过的边的数量。
- 节点的深度(depth):从根节点到该节点所经过的边的数量。
- 节点的高度(height): 从距离该节点最远的叶节点 到该节点所经过的边的数量。
请注意,我们通常将“高度”和“深度”定义为“经过的边的数量”,但有些题目或教材可能会将 其定义为“经过的节点的数量”。在这种情况下,高度和深度都需要加 1 。
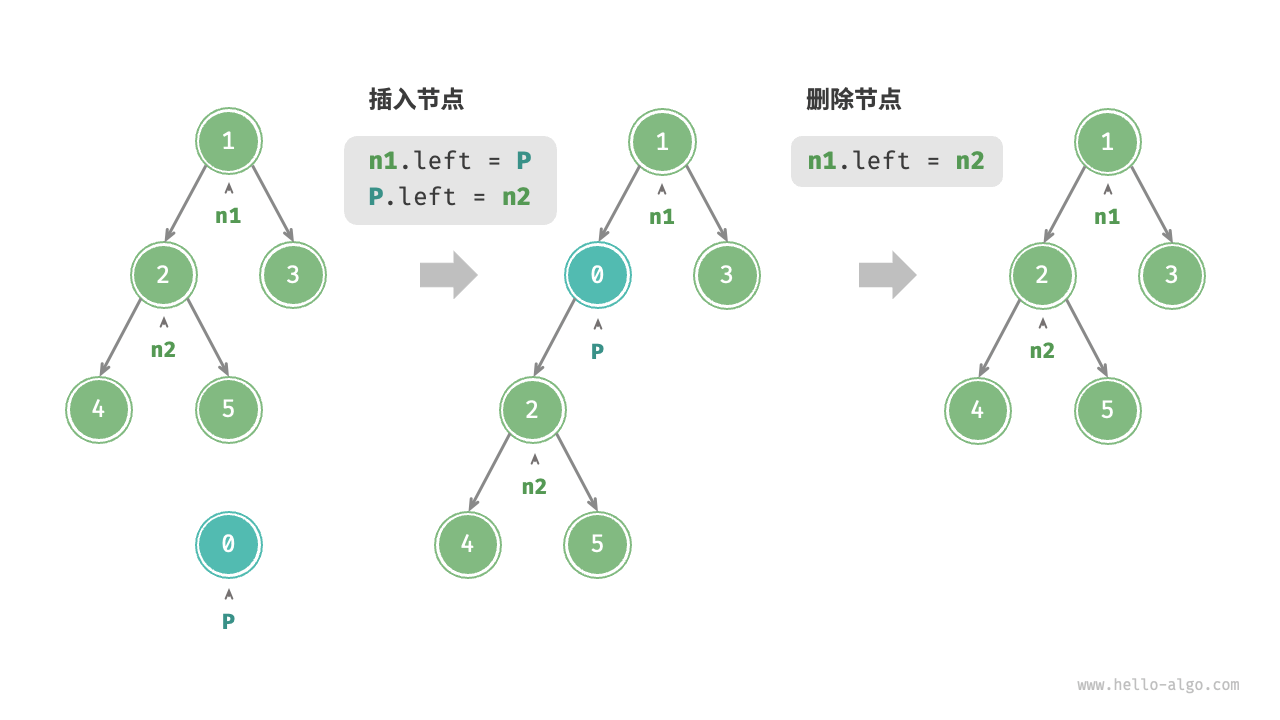
插入与删除节点
插入节点可能会改变二叉树的原有逻辑结构,而删除节点通常意味着删除该节点及其所有子 树。因此,在二叉树中,插入与删除通常是由一套操作配合完成的,以实现有实际意义的操 作。
常见二叉树类型
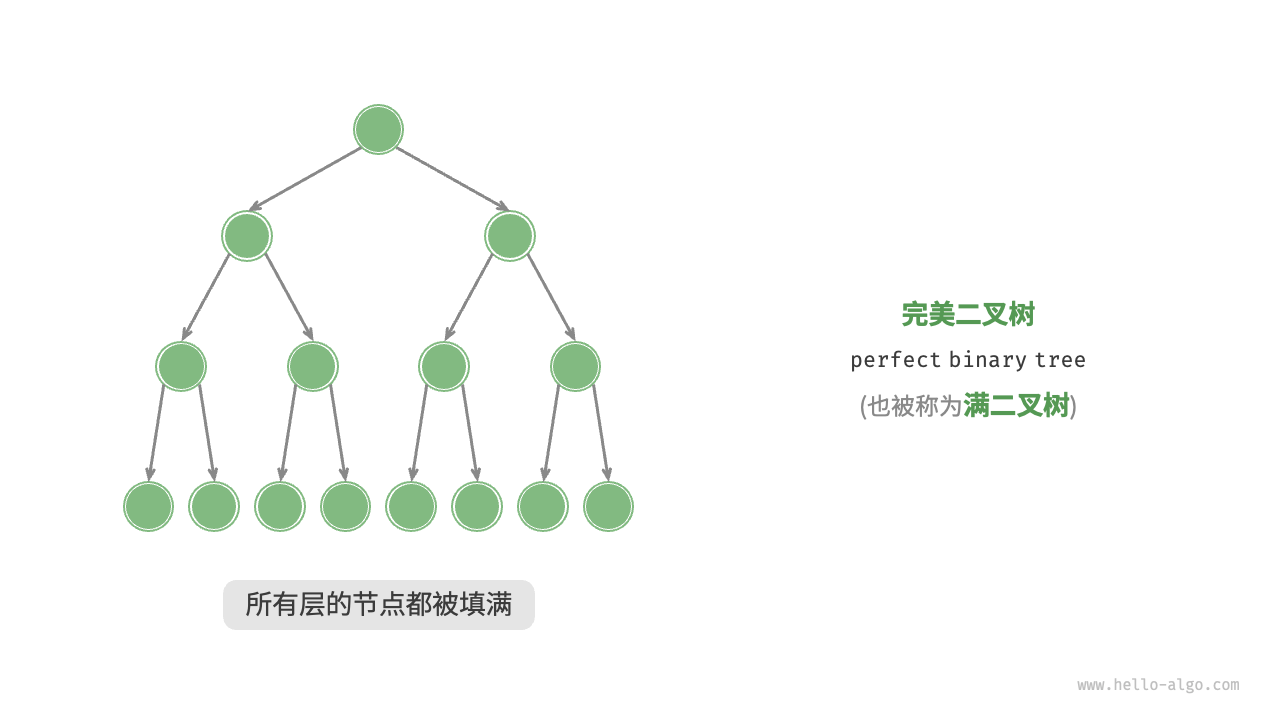
完美二叉树
完美二叉树(perfect binary tree)所有层的节点都被完全填满。在完美二叉树中,叶节
点的度为 0 ,其余所有节点的度都为 2 ;若树的高度为 h ,则节点总数为 2^{h+1} - 1
,呈现标准的指数级关系,反映了自然界中常见的细胞分裂现象。
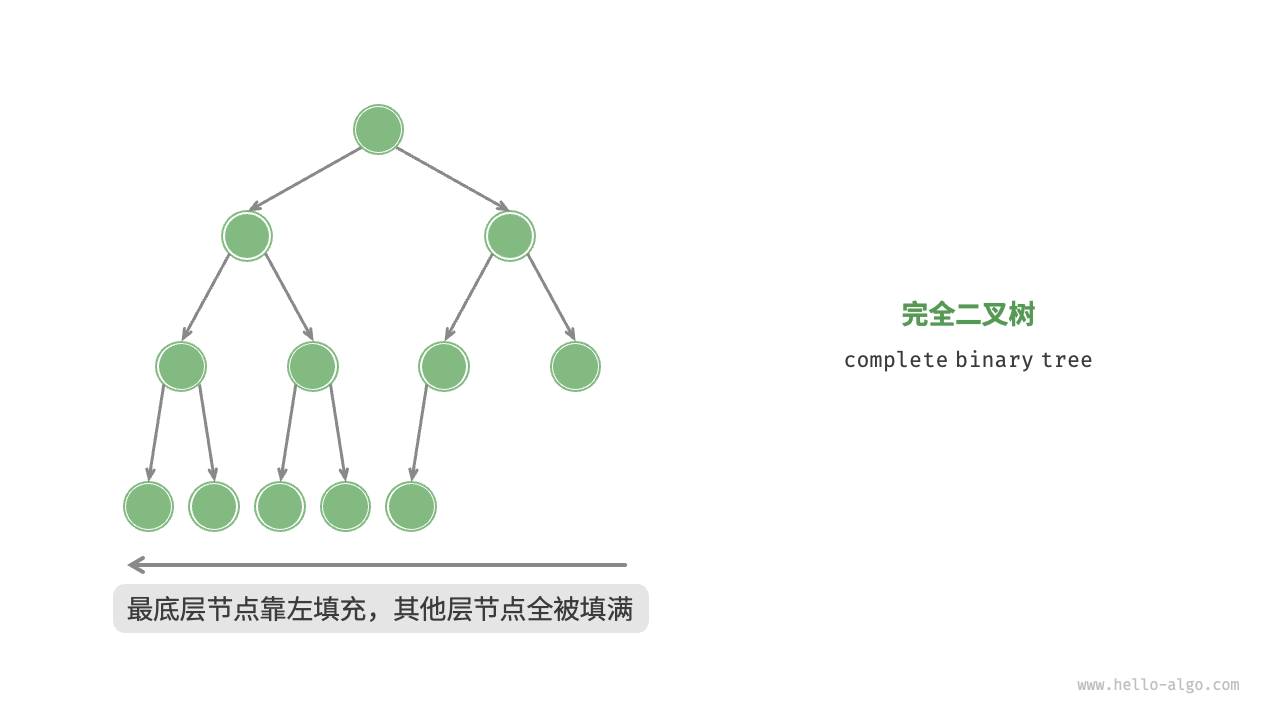
完全二叉树
完全二叉树(complete binary tree)只有最底层的节点未被填满,且最底层节点尽量靠左填充。
完满二叉树
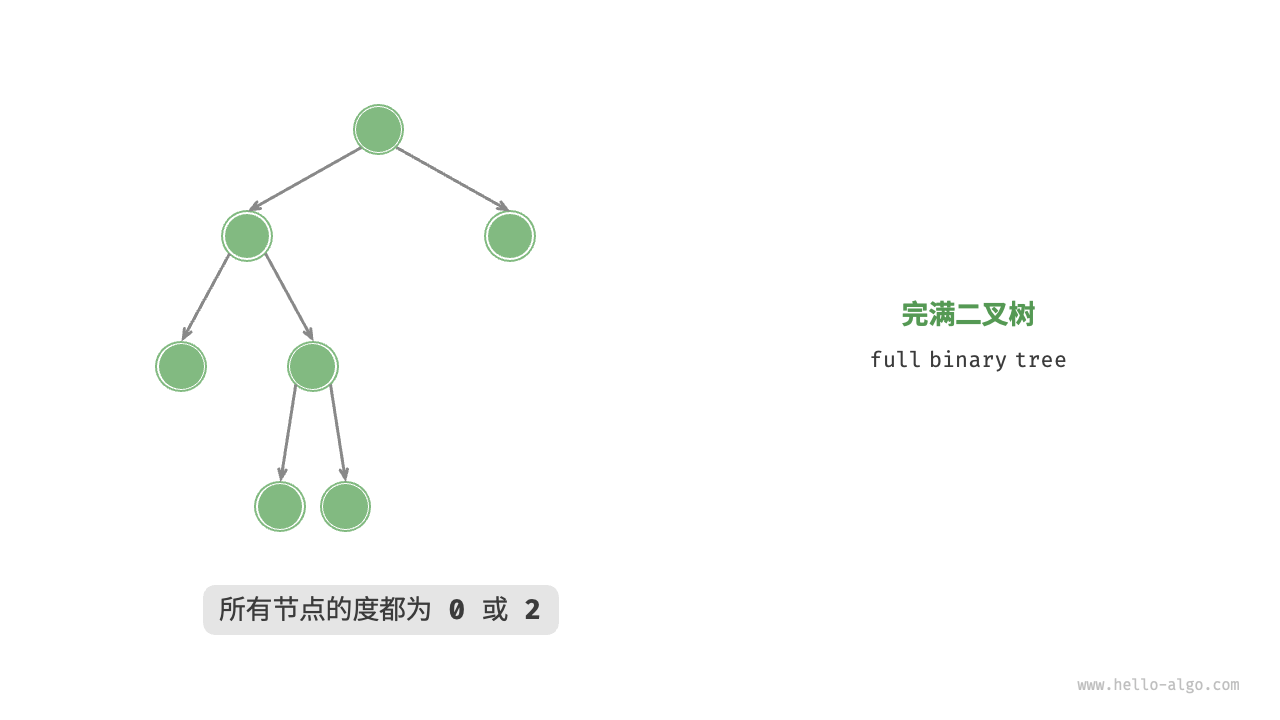
完满二叉树(full binary tree)除了叶节点之外,其余所有节点都有两个子节点。
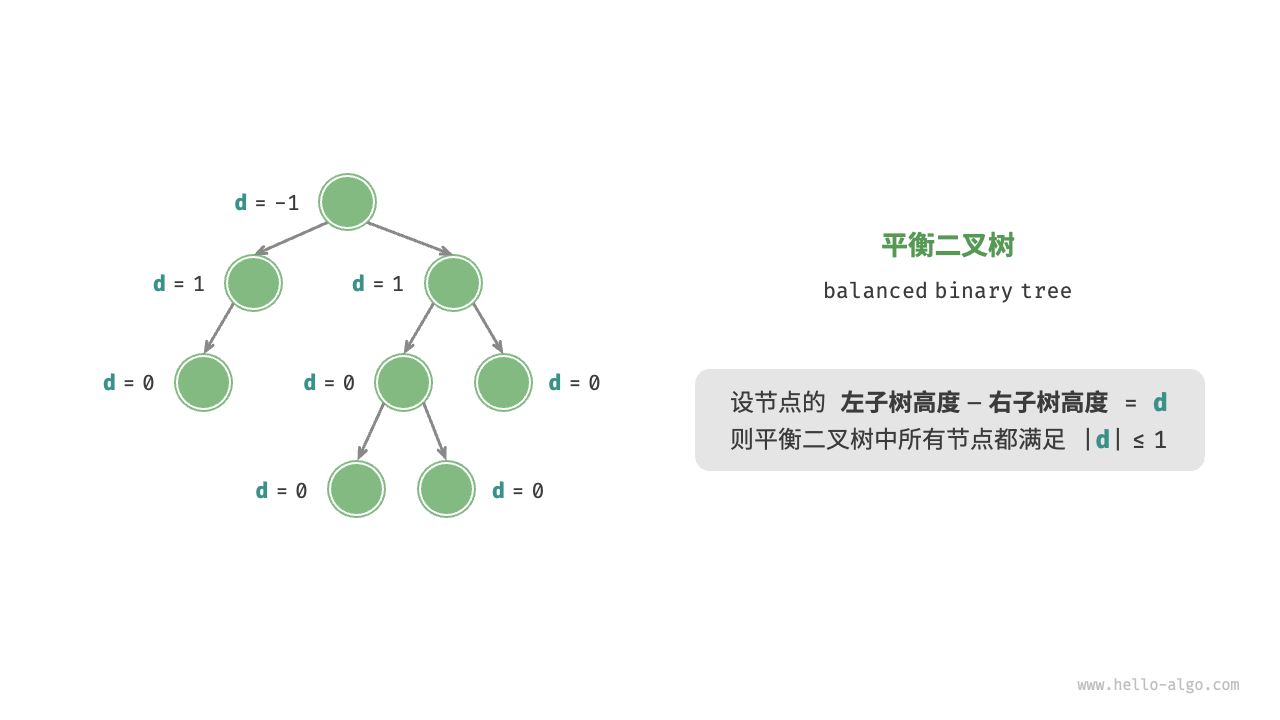
平衡二叉树
平衡二叉树(balanced binary tree)中任意节点的左子树和右子树的高度之差的绝对值不 超过 1 。
二叉树的退化
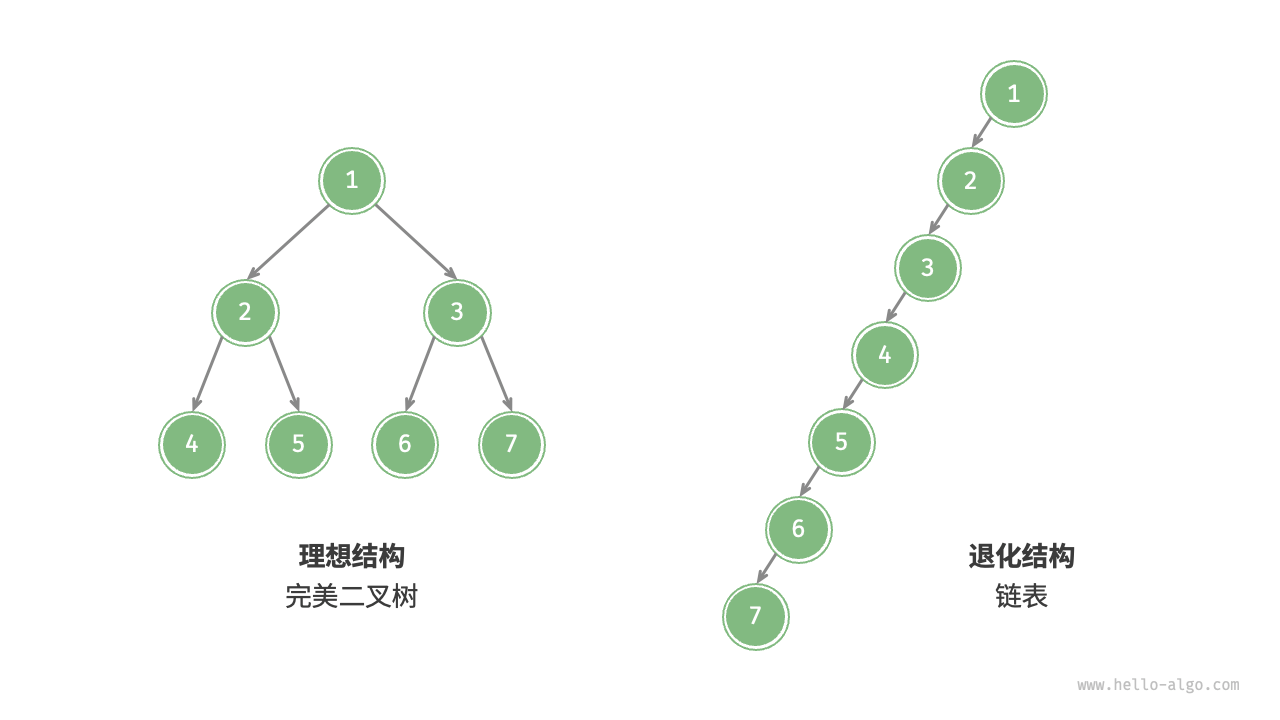
当二叉树的每层节点都被填满时,达到“完美二叉树”;而当所有节点都偏向一侧时,二叉树 退化为“链表”。
- 完美二叉树是理想情况,可以充分发挥二叉树“分治”的优势。
- 链表则是另一个极端,各项操作都变为线性操作,时间复杂度退化至
O(n)。